Fibonacciho posloupnost neboli „zlatá spirála“: Proč je tato řada čísel tak významným počinem? Jde o stavební kameny přírody

Fibonacciho posloupnost je jednoduchá řada čísel 1, 1, 2, 3, 5, 8, 13, 21 a tak dále. Každé číslo v této řadě je tvořeno součtem dvou předchozích. Další bude tedy 34 (21+13). Jde o nejjednodušší příklad rekurzivní posloupnosti, kde je každý člen tvořen rovnicí obsahující předchozí čísla v řadě. Tato matematická řada ovšem skrývá ještě další důležitou matematickou konstantu, tedy zlatý řez. A ten najdeme všude.

Nejdůležitější číslo ve vesmíru?

Někomu možná naskočí 42, ale tentokrát půjde o poměr. Konkrétně poměr s hodnotou přibližně 1,618: 1. V řecké abecedě, respektive alfabétě, je zlatý řez označen písmenem pí a stejně jako číslo pí má nekonečný počet desetinných míst bez jakýchkoli vzorců. Zlatý řez vznikne rozdělením úsečky na dvě části tak, že poměr větší části k menší je stejný jako poměr celé úsečky k větší části. Hodnota tohoto poměru je pak iracionální číslo.

iZdroj fotografie: Se souhlasem Marcus du Sautoy

Mnoho umělců považuje právě tento poměr za perfektní proporce plátna. Pokud vydělíte číslo ve Fibonacciho posloupnosti předchozím číslem v řadě (například 5/3), pak se zlomek s rostoucí hodnotou čísel stále více přibližuje právě zlatému řezu. S touto řadou se pojí nejrůznější záhady. Například, jestli je v ní také nekonečný počet prvočísel jako 2,3, 5 a 13. Známe jich zatím jen 51, ale mohlo by jích být nekonečně mnoho?

Proč jsou tato čísla tak důležitá?

Jde o oblíbená čísla přírody, která najdete všude po celém přirozeném světě. Pokud spočítáte okvětní lístky, je to většinou něco z této posloupnosti. A pokud ne, nejspíš nějaký odpadl (což je také způsob, jak se matematici vyhýbají výjimkám). Rozřízněte nějaké ovoce a najdete hvězdný tvar s Fibonacciho počtem ramen. Banán je má má 3, jablko 5, tomel 8. Semínka slunečnic projevují počty z té samé posloupnosti.

iZdroj fotografie: Se souhlasem Marcus du Sautoy

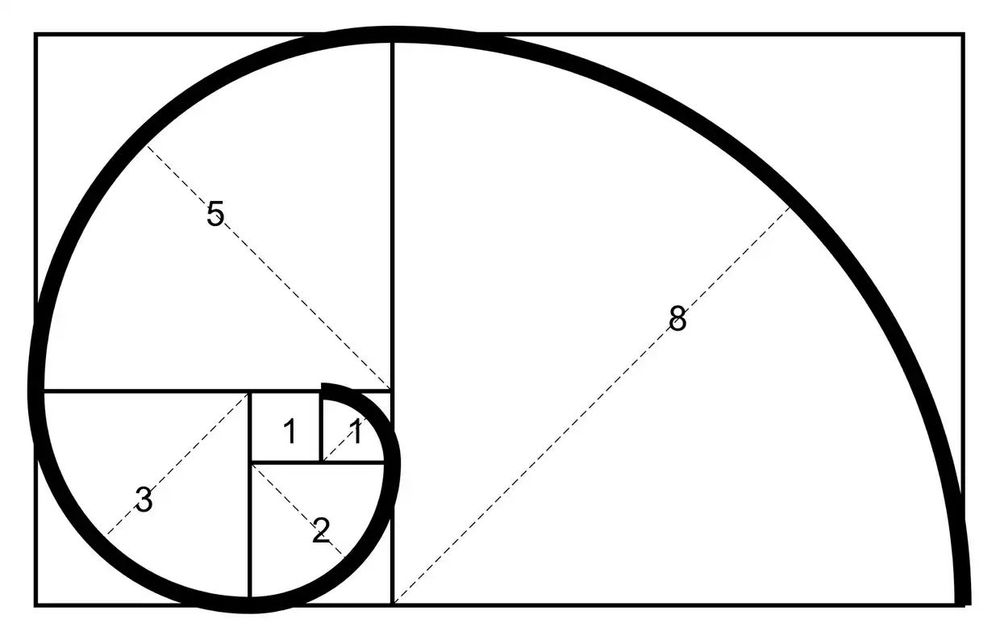
Fibonacci vysvětloval, že tato čísla jsou srdcem konstrukce světa. Příroda využívá to, co dosud vyrostlo, pro svůj další pohyb. Pokud vezmete čtverce s Fibonacciho rozměry, pak je můžete pospojovat do rostoucích obdélníků. To ukazuje, jak mohou věci narůstat a následně tvořit spirály. Podle stejných čísel roste i populace králíků. Pár králíků během měsíce dospěje, aby mohl dál plodit, kolik párů tu bude každý měsíc? Odpovědí je opět tato řada.

Kdo byl vlastně Fibonacci?

Číselná řada je pojmenována po italském matematikovi ze 13. století z Pisy. Byl znám také jako Leonardo Bonacci a do roku 1853 byl poměrně neznámý. Tehdy mu historik Guillaume Libri začal říkat Fibonacci. O těchto čísel napsal ve velmi vlivném spisku Liber Abaci, který byl vydán roku 1202. Záměrem knihy bylo pomoci s novými způsoby výpočtů a vysvětlit sílu nových arabských čísel. O těch se dověděl při cestě do Severní Afriky.

Jejich použití však vyžadovalo dovednost, takže tyto výpočty nebyly dostupné pro běžné obyvatelstvo. Místo použití nešikovných římských číslic Fibonacci vysvětlil, jak Indové využili čísla 1 – 9 společně s novým a revolučním konceptem nuly. Svazek dal běžnému lidu možnost počítat a také schopnost tyto výpočty zaznamenat. To je také důvod, proč byl tento záměr původně zakázán vládními činiteli i církevními kleriky.

Objevil je Fibonacci jako první?

Nikoli. Tato čísla by se ve skutečnosti měla jmenovat podle básníků a hudebníků, kteří je objevili stovky let před Fibonaccim. Bylo to právě pochopení rytmu hudby a poezie, které bylo jejich tajemstvím. Kolik různých rytmů můžete například vytvořit v bubnování, pokud budete kombinovat dlouhé a krátké údery? Ano, bude to Fibonacciho číslo. Mnoho moderních hudebníků si užívá používání právě těchto čísel při své tvorbě.

iZdroj fotografie: Pxhere

Například francouzský skladatel Claude Debussy je použil v Moři (La Mer) stejně tak maďarský skladatel Béla Bartok. Existuje i speciální forma poezie, tzv. Fib, kde slabiky na každé řádce odpovídají právě Fibonacciho číslům. Kromě využití v umění se stala i motivem šifer a záhad. Například v románu Šifra Mistra Leonarda od amerického spisovatele Dana Browna. Tam byla použita jako návod k otevření bezpečnostní schránky.

Jaké další matematické posloupnosti znáte a máte rádi?

Zdroj: SciShow