Tyto úlohy jsou běžným zadáním pro žáky 5. tříd, ale většině dospělých dělají problém. Jak jste na tom vy?
Geometrické úlohy jsou klasikou na ověření vaší vnímavosti. Porazí vás následující testy, nebo projdete na výbornou?

Vědeckého statusu se geometrie dočkala ve starověku, konkrétně v Řecku. Jejím primárním účelem byly ale věci zcela praktické, hlavně využití v zemědělství a stavebnictví. Vědecká obec tehdy ovšem řešila například otázky konstrukce různých geometrických útvarů. Během období středověku byla geometrie značně ovlivněna astronomii. Tím byla rozvinuta sférická geometrie. Použití v malířství vedlo k objevu perspektivy a projektivní geometrii.
Polopřímka, tečna, sečna
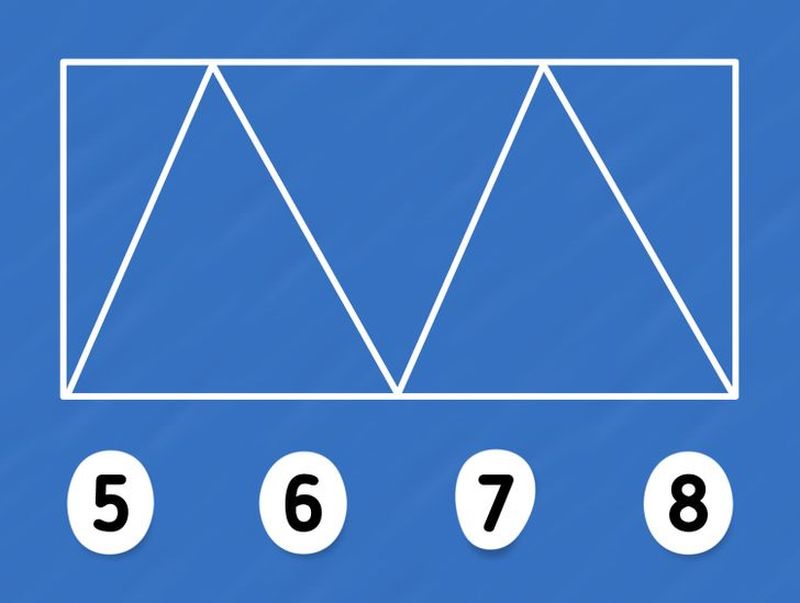
Několik slov z úvodu filmu pro pamětníky Škola, základ života nás do geometrického světa také zavádí. Základem je totiž geometrický útvar. Ten je souhrnem geometrických objektů, v první řadě bodů, přímek a rovin. Obvykle se toto spojení používá pro tvar nebo typ objektu, který je pojmenován – bod, přímka, prostor, trojúhelník nebo čtverec. A právě trojúhelníky budou dnes hlavními aktéry – kolik jich najdete v tomto obrázku?
Dalšími příklady jsou třeba křivka, prostorový úhel, fraktál nebo mezikruží. Během středověku rozvíjeli geometrii i další vědní disciplíny ve velké míře hlavně Arabové. Byly formulovány trigonometrické tabulky a zásluhou arabského astronoma al-Battániho se objevily první poznatky ze sférické trigonometrie. Mnohé geometrické útvary lze dodnes najít v islámské architektuře, třeba jako dekorace složené z dlaždic.
Descartes a novověká geometrie
Během 17. století přidal slavný francouzský filosof René Descartes (autor Rozpravy o metodě) do geometrie systém souřadnic. Tak byly položeny základy pro analytickou geometrii, která dovoluje vyjádření geometrických útvarů za pomoci rovnic. To také dovoluje řešit související problémy cestou analytiky a algebry. Díky Gottfriedu Leibnizovi a Isaacu Newtonovi vznikl integrální počet. Kolik trojúhelníků najdete na tomto obrazci?
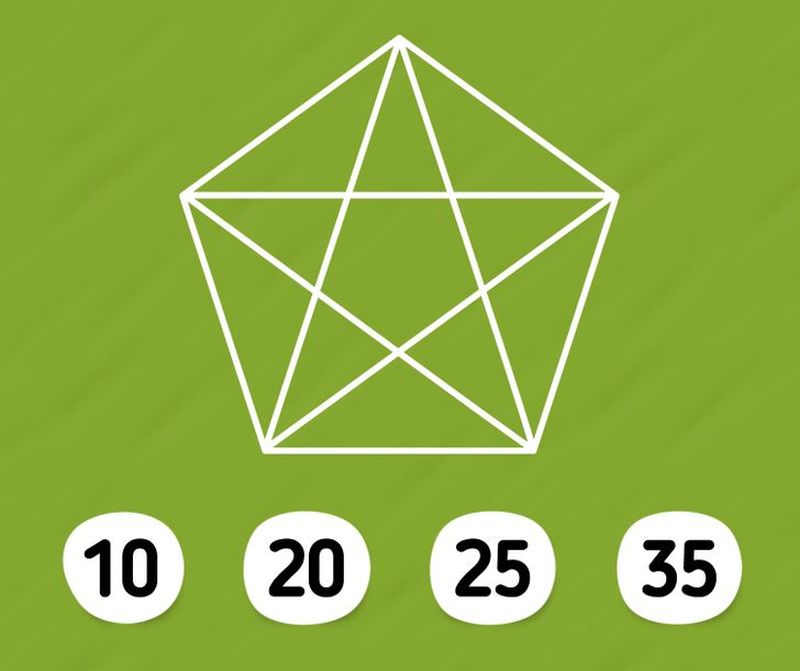
Geometrie je jeden z oborů se stálým vývojem, dokonce i během 20. století. Vliv má i to, že je velmi propojena s dalšími obory, a studium problémů pravděpodobnosti vedlo také ke vzniku pojmu informační geometrie. Pokud stále tápete, pak vězte, že na prvním obrazci se skrývá 5 trojúhelníků a na obrazu pentagramu je jich dokonce 35. Ano, je opravdu třeba dávat si pozor a počítat všechno, co tvoří trojúhelník. Tvary se totiž velmi rády překrývají.
Kolik trojúhelníku jste dohromady objevili?




