Troufnete si na matematický příklad z 50. let? Málokdo dokáže tento problém vyřešit bez použití kalkulačky
Matematická otázka z 50. let způsobila při svém online vypuštění značný rozruch. Většina lidí ji totiž nedokáže vyřešit bez využití digitální pomoci, tedy kalkulačky.
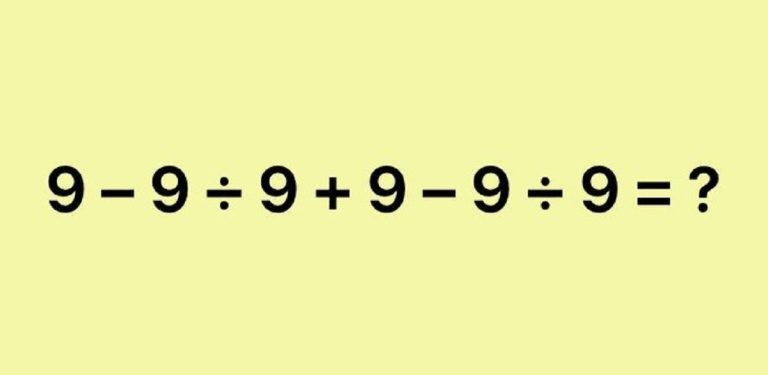
Obsah článku
Nejspíš si na první dobrou myslíte, že je to jedna z těch obtížných otázek, která se sem tam objeví a každý na ni může mít zcela jinou odpověď. Tohle je ovšem situace opačná. Nejspíš jste se s podobným příkladem setkali už na základní škole. Pokud si v základní matematice nejste příliš jistí v kramflecích, je tohle dobrá možnost, jak si to ověřit. Vypadá to totiž jednoduše, jde však o jeden z nejobtížnějších matematických problémů.
Odpověď má jasnou strukturu
Pořád cítíte vlastní sebevědomí? Online řešitelé totiž přišli pokaždé s jiným výsledkem. Ve skutečnosti se ovšem jedná o prostý problém priority početních operací a správný výsledek je jen jeden. Společně s počtem protichůdných odpovědí se samozřejmě množilo sdílení tohoto příkladu, až se logicky stal virálním. Tak co, už jste si s tím poradili? Pokud jste odpověděli 0, 4, 7 nebo desetinný zlomek, raději se na to podívejte ještě jednou.

Berte to jako mozkovou výzvu. Přestože vám může připadat značně otravná, jde o zajímavý způsob tréninku paměti a také schopnosti zpracovat informace. Pojďme si zatím říct něco o původu priority početních operací neboli anglicky PEMDAS. Není to jen eukleidovská matematika a Pythagoras. Postupné řešení umocňování a odmocňování, násobení a dělení, sčítání a odčítání se přece jen někde vzít muselo, že? Pravda, skutečný původ je nejasný.
Postupně rostoucí nároky na matematiku
Někteří historici uvádí, že pořadí operací vzniklo z jednoduché a zoufalé potřeby zjednodušeného řešení. Už někdy v 6. století před Kristem potřebovali lidé matematiku pro mnoho účelů. Počítat zvířata, úrodu a také kvůli obchodování. Mnoho komunit si nevyhnutelně vyvinulo vlastní početní systémy. Například v Babylonu se ujal systém odvozený od čísla 60, zatímco valná většina měřila v desítkách. Prvotní operace byly jen sčítání a odčítání.

Je ale jasné, že tyto základy byly časem zcela nedostatečné. Jakmile se dostalo na rychlé a opakované přidávání stejného počtu, zrodilo se násobení. K němu byl samozřejmě třeba i úkon opačný – a máme tu dělení. Po stovky let byly tohle jediné operace, které matematika obsahovala. Priorita početních operací se stala konvencí tehdy, když se lidé potřebovali v matematice dostat k jednotnému výsledku. Stanovili proto jasnou metodu, jak postupovat.
Definice priority početních operací
Výsledkem je, že nejdříve jsou řešeny části v závorkách. Následují mocnění a odmocňování. Poté přijde na řadu násobení a dělení a nakonec prosté sčítání a odčítání. Postupuje se tedy od složitých operací k těm jednodušším. To už lze řešit zleva doprava včetně záměn bez přesného pořadí.
Správné řešení tohoto problému
9 – (9 / 9) + 9 – (9 / 9) = ?
9 – (1) + 9 – (1) = ?
Pak se přesuneme ke sčítání a odčítání normálně zleva doprava:
9 – 1 + 9 – 1 = ?
8 + 9 – 1 = ?
17 – 1 = 16




